Processing math: 14%

Undergraduate and Applied MSc Projects

Below are the lists of possible undergraduate/Applied MSc Projects, all of which require a combination of designing and/or implementing numerical methods and performing applied analysis.

Travelling wave solutions for nonlocal bistable reaction-diffusion equation
Applications of scaling symmetry in differential equations
Compact finite difference schemes
Geometric numerical integration of ODEs
Pattern formation of Reaction-diffusion equations with chemotaxis
Pattern formation of Reaction-diffusion equations with sea shells or sand dune
Numerical solution of second order ODEs on the complex plane
Love's integral equation

You can also find some Past project reports here, just to get some idea how it should look like.

Travelling wave solutions for nonlocal bistable reaction-diffusion equation

In this project, travelling waves solutions for the following non-local bistable reaction-diffusion equation $\frac{\partial}{\partial t}u = J\ast u -u +f(u)$ is studied. Here $J$ is a non-negative, continuously differentiable function such that $\int_{\mathbb{R}} J(x)dx=1, \int_{\mathbb{R}} |x|J(x)dx<\infty$ with the typical examples $J(x)=\max(0,1-|x|)$ or $J(x) = \exp(-\pi x^2)$ , $J\ast u(x) = \int_{\mathbb{R}} J(x-y)u(y)dy$ is the convolution between $J$ and $u$ and $f(u)=F'(u)$ is the derivative of a double-well potential $F(u)$ . Both numberical solutions and qualitative properties of the travelling waves will be investigated.

References:

X. Chen, "Generation, propagation, and annihilation of metastable patterns", J. Differential Equations 206, 399–437 (2004).
Bates, Peter W., Paul C. Fife, Xiaofeng Ren, and Xuefeng Wang. "Traveling waves in a convolution model for phase transitions." Archive for Rational Mechanics and Analysis 138, no. 2 (1997): 105-136.

Applications of scaling symmetry in differential equations

Scale invariance is ubiquitous in mathemtics and physics, as a feature of the underlything qunatity which changes in a simple predictable way when other variables changes by a common factor. In this project, scaling symmetry(or scaling invariance) is explored in several applications related to differential equation: self-similarity and self-similar solutions, conserved quantities and commuting flows of nonlinear equations, exact solutions of equations with scaling symmetries.

References:

Barenblatt, Grigory Isaakovich. Scaling, self-similarity, and intermediate asymptotics: dimensional analysis and intermediate asymptotics. Vol. 14. Cambridge University Press, 1996.
Barenblatt, Grigory Isaakovich. Scaling. Vol. 34. Cambridge University Press, 2003.
Goktas, Unal, and Willy Hereman. "Invariants and symmetries for partial differential equations and lattices." arXiv preprint solv-int/9801024 (1998).
Dresner, Lawrence. Applications of Lie's theory of ordinary and partial differential equations. CRC Press, 1998.

Compact finite difference schemes

In general, higher order finite difference schemes for ordinary/partial differential equation require a wider stencil. For instance, the classical three point scheme for the simplest second order ODE

$u''(x) = f(x)$ is

$\frac{u_{j+1}-2u_j+u_{j-1}}{h^2} = f_j$ where

$h$ is the grid size such that

$x_j = jh$ ,

$f_j=f(x_j)$ and

$u_j$ is the numerical approximation of

$u(x_j)$ . This scheme is only second order accurate in the sense that the error

$|u_j-u(x_j)|=O(h^2)$ , while a higher order scheme (say 4th order) looks like

$\frac{-u_{j+2}+16u_{j+1}-30u_j+16u_{j-1}-u_{j-2}}{h^2} = f_j,$ whose stencil consists of five points. Compact finite difference schemes are higher order numerical methods that use less points in the stencil. In this project, two diretions will be reviewed and explored (one is fine for sinle project). The first approach is to modify the original lower order schemes to eliminate leading order truncation error, such as the 4th order scheme

$\frac{u_{j+1}-2u_j+u_{j-1}}{h^2} = \frac{f_{j+1}+10f_j+f_{j-1}}{12}$ using only three points. The second approach is to introduce new variables for the time derivatives, by sovling a larger system of discrete equations.

References:

Lele, S. K. (1992). Compact finite difference schemes with spectral-like resolution. Journal of computational physics, 103(1), 16-42.
Deng, X., & Maekawa, H. (1997). Compact high-order accurate nonlinear schemes. Journal of Computational Physics, 130(1), 77-91.

Geometric numerical integration of ODEs

In this project, a special class of numerical methods for ordinary differential equations (ODEs) will be studied. These methods focus on preserving the qualitative properties like the conservation of first integrals and large time asymptotic behaviours. The interested student should have taken Numerical Analysis II and be comfortable writing code (MATLAB is preferred).
References:

Hairer, Ernst; Lubich, Christian; Wanner, Gerhard (2002). Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations. Springer-Verlag.
Ben, Leimkuhler; Sebastian, Reich (2005). Simulating Hamiltonian Dynamics. Cambridge University Press
Iserles, Arieh. A first course in the numerical analysis of differential equations. No. 44. Cambridge university press, 2009.

Pattern formation of Reaction-diffusion equations with chemotaxis

Many existing equations in pattern formation, like the well-known Gray-Scott system or Gierer-Meinhardt system, usually consist of two component (activator-substrate or activator-inhibitor). In this project, a three-component system proposed in [1] is further studied, using the numerical method proposed in [2], to clarify the following questions:

The dependence of the pattern on the parameters
Construction of the spike solutions (see the figures below) using singular perturbation
Possible reduction of the original equations in [1] to understand the key terms and mechanisms for the the pattern formation

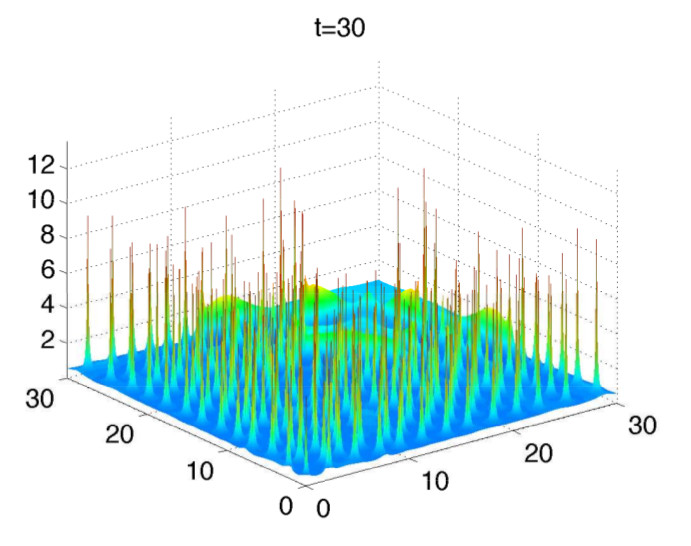
References:

R Tyson, SR Lubkin, James D Murray. A minimal mechanism for bacterial pattern formation. Proceedings of the Royal Society of London B: Biological Sciences 266(1416): 299-304. 1999
A Chertock, A Kurganov. A second-order positivity preserving central-upwind scheme for chemotaxis and haptotaxis models. Numerische Mathematik 111(2), 169-205

Pattern formation of Reaction-diffusion equations with sea shells or sand dune

Many existing equations in pattern formation, like the well-known Gray-Scott system or Gierer-Meinhardt system, usually consist of two component (activator-substrate or activator-inhibitor). In this project, the patterns of sea shells or sand dune will be studied:

examinine the underlying modelling assumptions
analyse the bifurcation of steady patterns
investigate the selection of length scales

References:

Meinhardt, Hans. The algorithmic beauty of sea shells. Springer Science & Business Media, 2009.
Hoyle, Rebecca B. Pattern formation: an introduction to methods. Cambridge University Press, 2006.

Numerical solution of second order ODEs on the complex plane

In this project, numerical solution of second order ODEs are extended from the real line (treated in standard textbooks) to the complex plane. Special methods based on Padé approximation may be preferred because of the possible poles in the solutions and other singularities like branch points. A family of ODEs called Painlevé transcendents will be studied. Working knowledge on complex variables and numerical methods for ODEs is essential.
References:

Corliss GF. Integrating ODEs in the complex plane—pole vaulting. Mathematics of Computation. 1980;35(152):1181-9.
Corliss G, Chang YF. Solving ordinary differential equations using Taylor series. ACM Transactions on Mathematical Software (TOMS). 1982 Jun 1;8(2):114-44.
Fornberg B, Weideman JA. A numerical methodology for the Painlevé equations. Journal of Computational Physics. 2011 Jul 1;230(15):5957-73.
Reeger JA, Fornberg B. Painlevé IV: A numerical study of the fundamental domain and beyond. Physica D: Nonlinear Phenomena. 2014 Jul 1;280:1-3.

Love's integral equation

The Fredholm integral equation o fthe second kind

$\begin{equation} f(x) = g(x) + \frac{1}{\pi}\int_{-L}^{L} \frac{f(t)}{(x-t)^2+1}dt \end{equation}$ arises in the calculation of electrosttic field of two equal circular conducting disks [2]. Existence numerical methods for solving Fredholm integral equations are surveyed, followed by some further studies on properties about the resolvent kernel and eigenvalues/eigenfunctions.

References:

L. Fox and E. T. Goodwin. The numerical solution of non-singular linear integral equations. Philos. Trans. Roy. Soc. London. Ser. A. 245, (1953). 501–534.
R. R Love. The electrostatic field of two equal circular co-axial conducting disks. The Quarterly Journal of Mechanics and Applied Mathematics 2, no. 4 (1949): 428-451.
P. Pastore. The numerical treatment of Love's integral equation having very small parameter. J. Comput. Appl. Math. 236 (2011), no. 6, 1267–1281.
K. E. Atkinson, and L. P. Shampine. Algorithm 876: solving Fredholm integral equations of the second kind in Matlab. ACM Trans. Math. Software 34 (2008), no. 4, Art. 21, 20 pp.

Past projects

Some past projects are listed here:

MSc Project, Travelling Wave Solutions , by Rami Achouri (Manchester 2016)
MSc project, Stationary densities of stable Levy flights in external potentials, by M. Leval (Imperial College 2015)
Second year group project, Gangs and Graffiti: A Statistical Mechanical Approach, by S. Dutt, B. Kinger, A. Leidiger and L. Mineh (Imperial College 2015)
Third year joint Math and Computer Science project, Finite Volume Schemes for Non- Linear Diffusion Equations, by H. Ostwal (Imperial College 2015)
Second year group project, Ising Model for Gang and Graffiti, by O. Ayouche, E. Lau, W. Liu and A. Magli (Imperial College 2014)