Tutorial on transforming hyperspectral imagesAn
introduction to
obtaining
radiance and RGB colour
|
1. Background
Hyperspectral images provide both spatial and spectral representations of scenes, materials, and sources of illumination. They differ from images obtained with a conventional RGB colour camera, which divides the light spectrum into broad overlapping red, green, and blue image slices that when combined seem realistic to the eye. By contrast, a hyperspectral camera effectively divides the spectrum into very many thin image slices, the actual number depending on the camera and application (Refs 1 and 2). This fine-grained slicing reveals spectral structure that may not be evident to the eye or to an RGB camera but which does become apparent in a range of visual and optical phenomena, including metamerism (Ref 3) and colour constancy (Ref 4).
To help understand its organisation, a hyperspectral image may be represented as a cube containing two spatial dimensions (pixels) and one spectral dimension (wavelength), as illustrated in Fig. 1. In this example (the original hyperspectral image is available here), the spectrum has been sampled at 10-nm intervals over 400-720 nm. At each sample wavelength, there is a complete intensity (grey-level) representation of the reflectance or radiance in the scene.
|
| Figure 1. Hyperspectral image cube |
The same data can be rendered as a conventional RGB colour image, as in Fig. 2. The effective spectral reflectances at selected pixels 1, 2, and 3 are indicated in Fig. 3.
 |
 |
|
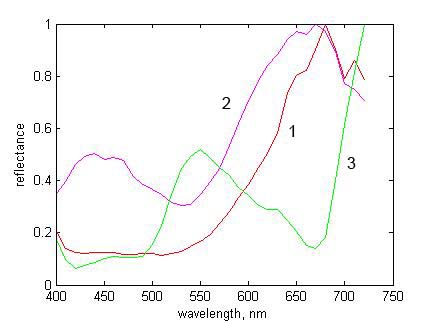Figure
2. RGB scene image
with three selected pixels
|
Figure
3. Normalized reflectances at selected pixels of Fig. 2 |
The aim of this tutorial is to show how hyperspectral images of reflectance data such as those downloadable here and here can be transformed into reflected radiance data and how, in turn, these radiance data can be transformed into RGB images.
Computations are performed in MATLAB (The MathWorks Inc.), which draws on the Matlab Image Processing Toolbox. Some supporting routines, data, and a test hyperspectral image are also needed, all of which can be downloaded as a 15 MB zipped package here.
This package should be unzipped into a directory on the MATLAB path. Some familiarity with elementary MATLAB operations and basic colour science is assumed. For an introduction to both, see Ref. 5.
ref4_scene4.mat is a test hyperspectral image consisting of an array of spectral reflectances of size 255 x 355 x 33. The first two coordinates represent spatial dimensions (pixels), in row-column format, and the third coordinate represents wavelength (400, 410, ..., 720 nm), as in Fig. 1. For ease of handling in this tutorial, the image has been reduced spatially to about a quarter of the size of those downloadable here.
illum_25000.mat, illum_6500.mat, and illum_4000.mat are three illuminant spectra, each vectors of length 33 (i.e. 400, 410, ..., 720 nm), representing the spectra of blue skylight with correlated colour temperature (CCT) 25000 K, daylight with CCT 6500 K, and evening sunlight with CCT 4000 K (from Ref. 6).
xyzbar.mat contains the CIE 1931 colour-matching functions (from Ref. 6).
XYZ2sRGB_exgamma.m is a routine for converting tristimulus values XYZ to the default RGB colour space sRGB, but without gamma correction . A copy of the document IEC_61966-2-1.pdf explaining the full conversion of XYZ to sRGB is also included.
Load
ref4_scene4.mat
and test the size of the resulting array reflectances.
load ref4_scene4.mat; |
It should
have size 255 x 335 x 33. To inspect reflectances,
try taking a slice at a
middle wavelength, say 560 nm (17th in the sequence 400, 410, , 720
nm), and displaying it. The image should look like Fig. 4
(except for
the added red square, left).
slice = reflectances(:,:,17); |
 |
 |
| Figure
4. Slice from
hyperspectral reflectance image at 560 nm |
Figure
5. As Fig. 4 with
intensity levels clipped to level in red square |
The
command brighten
is used to
compensate roughly for the gamma of the monitor or display (i.e.
the
nonlinear input-output function), and an equivalent effect can be
produced with slice.^0.5,
or
slice.^0.4,
in place of slice
as the
argument to imagesc.
The image
still
appears dark, however, because the exposure used during image
acquisition by the
hyperspectral camera was determined by the specular highlight at the
top right of
the scene. For presentational purposes, therefore, the intensity levels
of the
image in Fig. 4
may be truncated by clipping to a level, z
say, of a less-specular
region (all intensity levels above z
are then set equal to z).
The clip level z
was taken from the
pixel with row-column coordinates (100, 39) in the red square. The
image should now look like
Fig. 5.
Detail in the darker areas is now much clearer than in
Fig. 4.
z = max(slice(100, 39)); |
Now choose a different pixel in the scene, say with row-column coordinates (141, 75), and plot its spectral reflectance. The plot should look like Fig. 6.
reflectance =
squeeze(reflectances(141, 75,:)); |
 |
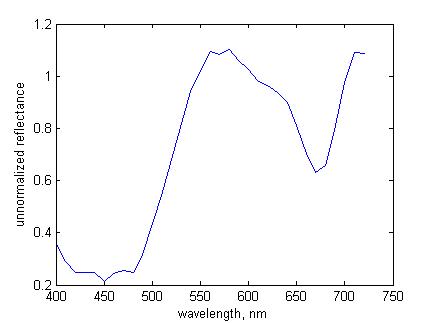| Figure
6. Unnormalized
spectral reflectance at pixel (141, 75) |
The
value of reflectance
exceeds unity at some wavelengths, as in Fig. 6.
This is
because the reflectances were normalized against an area on the grey
sphere at the bottom of the image, and the intensity of light reflected
from some other surfaces, at different angles, is
greater, e.g.
at
the pixel with row-column coordinates (100,
39). The array reflectances
may
be normalized by dividing by the maximum reflectance taken
over all pixels and wavelengths.
reflectances =
reflectances/max(reflectances(:)); |
For more a detailed explanation of normalization, see Section 6.2 later; also the Notes section here and Appendix A of Ref. 3.
Load one of the illuminant spectra, say
illum_25000.
Multiply
each
reflectance in the scene by this illuminant spectrum to get the
reflected
radiances radiances_25000
(a for-loop
is less
efficient than MATLAB's bsxfun
function, but it makes little difference here). Using the same pixel as for Fig. 6,
plot the reflected
radiant spectrum radiance_25000
(notice
the different spelling). The spectrum
should look like curve 1 in Fig. 7.
load illum_25000.mat; |
Repeat with another
illuminant spectrum, e.g. illum_4000.
The reflected radiance spectrum should look like curve 2 in Fig. 7.
Notice how the reflected spectra differ
from each other
and from the spectral reflectance in Fig. 6.
load illum_4000.mat; |
 |
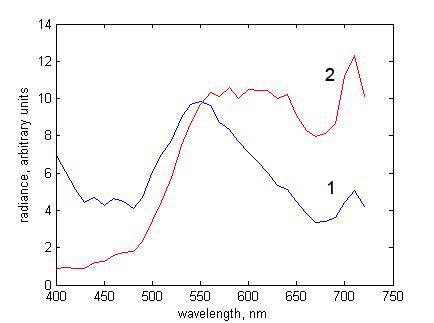| Figure
7. Reflected
radiance spectra at pixel (141,
75) for illuminants with CCTs (1) 25000
K and (2) 4000
K |
Load the
illuminant spectrum illum_6500
and obtain reflected
radiances radiances_6500.
load illum_6500.mat; |
Record the size of the array radiances_6500,
and then reshape it as a matrix of w
columns for matrix multiplication
with the colour-matching functions.
[r
c w] =
size(radiances_6500); |
Load the CIE 1931 colour
matching
functions xyzbar
and take
the matrix product of xyzbar
with radiances
to get the tristimulus values XYZ
at
each pixel. For simplicity XYZ
is not
normalized.
load xyzbar.mat;
|
Correct the shape of XYZ
so
that it
represents the original 2-dimensional
image
with three planes (rather than a matrix of 3
columns), and ensure
that
the
values of XYZ
range
within 0-1.
XYZ
= reshape(XYZ, r, c, 3); |
To convert this XYZ
representation of the image to the default RGB
colour representation sRGB (IEC_61966-2-1), excluding
any
gamma correction, apply the transformation XYZ2sRGB_exgamma.
Ensure
that the RGB
values range within 0-1 by clipping to 0
and 1 (or, if
they greatly exceed 1, perhaps scaling by the maximum).
RGB
= XYZ2sRGB_exgamma(XYZ); |
Finally, display the RGB image, including a rough gamma correction. The image should look like Fig. 8 (except for the added red square, bottom left).
figure;
imshow(RGB.^0.4, 'Border','tight');
|
|
|
 |
| Figure 8. RGB image of reflected radiance | Figure
9. As Fig. 8
but with
intensity levels clipped to level in red square |
The image appears dark for the same reason mentioned in Section 3, namely the hyperspectral camera exposure having to accommodate the specular highlight on the top right. Again for presentational purposes, the RGB levels of the image may be uniformly truncated by clipping to the level of a less-specular region. The clip level was taken from the pixel with row-column coordinates (244, 17) in the red square on the grey sphere. The image should now look like Fig. 9. As with Fig. 5, detail in the darker areas is now much clearer. The same procedure may be used to obtain sRGB images with the other two illuminant spectra with CCTs of 25000 K and 4000 K.
z
= max(RGB(244,17,:)); |
Sample spectra from natural scenes recorded with a hyperspectral camera may appear less smooth than spectra from single pigments recorded with a spectroradiometer in the laboratory. The reason is that the physics of the two situations is very different. Natural scenes usually are complex, have non-uniform illumination, and are recorded remotely by the camera, whereas laboratory pigment spectra usually are simple, have uniform illumination, and are recorded with a non-imaging device that averages signals over large homogeneous areas of the specimen. Where imaging conditions coincide, hyperspectral imaging and spectroradiometric data can match closely (see e.g. spectra of acrylic paints imaged under laboratory illumination in Fig. 1 of Ref. 3).
The complexity of natural spectra is due to several factors.
1. Many natural scenes contain foliage, and foliage contains pigments such as chlorophylls and carotenoids, and anthocyanins in autumn, which give multiple large and small absorbance peaks distributed over the visible spectrum (see e.g. Ref. 7). Depending on the particular combination of these pigments, their presence can produce a variety of complex reflectance spectra from region to region.
2. There are important physical surface effects associated with foliage reflection (Refs 8 and 9), which cause the reflected spectrum to vary markedly across different microscopic areas. More generally, natural organic and inorganic materials are likely to be spatially nonuniform, and may be contaminated by dirt and moisture, which along with weathering and biological degredation contribute to the complexity of the recorded spectrum.
3. Natural illumination is often variegated. Direct illumination from the sun may be combined with indirect illumination from the sky, together with local nonlinear mutual illumination, transillumination, and occlusion.
A further complication with hyperspectral imaging of natural scenes comes from having to limit the camera exposure duration to avoid the effects of fluctuating illumination and movement within the scene. For a combination of reasons, the signal-to-noise ratio may be low at the extremes of the visible range. In particular, the transmittance of the tunable liquid crystal filter used in some hyperspectral imaging devices is poorest at short wavelengths, where the incident radiant power from the sun is also least. Image slices at 400 nm may be particularly noisy (see examples here and here).
The spectral reflectance of a surface element in a hyperspectral image is defined essentially as the quotient of the recorded radiant spectrum by the recorded radiant spectrum from a neutral matt reference surface embedded in the scene, multiplied by the known spectral reflectance of the reference surface (Ref. 3, Appendix A). From these effective spectral reflectance values, spectral radiance values can be recovered as outlined in Section 4.
Some of the spectral reflectance values available here and here exceed unity (also as in Fig. 6 here), despite the image being normalized with respect to a reference surface in the scene, usually a well-illuminated area (although see e.g. Fig. 2, bottom right). These excessive spectral reflectance values are a result of the optics of the scene and are intrinsic to these radiance calculations.
1. Excessive spectral reflectance values are due mainly to the nature of the bidirectional reflectance distribution function (BRDF) sampled by the scene and camera geometry. Thus when the reference surface is flat, it is almost always oriented with its surface normal towards the camera and away from the sun. But other surfaces in the scene may be oriented more favourably and be capable of reflecting more light to the camera. Even when the reference surface is spherical so that there is an optimal surface normal at some point (e.g. Fig. 8, bottom left), specular reflections from other surfaces in the scene may reflect more light to the camera (e.g. from water, as in Fig. 8, top right).
2. As explained in the Notes section here, excessive spectral reflectance values are not important for a given scene and camera geometry, since it is the estimation of the reflected spectral radiance that matters. But for the analysis of the spectral reflectances themselves, it may be best to uniformly scale all the spectral reflectances in a hyperspectral image so that the greatest value does not exceed unity (Section 3, end). Unlike the manipulations for image presentation (Figs 5 and 9), spectral reflectances should not be scaled by ranked pixel values, e.g. the 90th or 99th centile, as this kind of clipping can substantially inflate both the spectral reflectance and accompanying noise estimates.
A fuller discussion of effective reflectances and effective illuminants is available in the Notes section here and in Appendix A of Ref. 3.
